A Paper Sizes
A Paper Sizes - A0, A1, A2, A3, A4, A5, A6, A7, A8, A9, A10 - http://www.papersizes.org/a-paper-sizes.htm
Information
Lichtenberg Ratio
A4 vs US Letter | Between Borders - http://betweenborders.com/wordsmithing/a4-vs-us-letter/
When people in the US and Canada reach for a sheet of paper to write or print on, chances are they reach for a piece of Letter-sized paper (also known as US Letter), measuring 8.5˝ by 11˝. With few exceptions, when people everywhere else reach for a sheet of paper to write or print on, they reach for a piece of A4-sized paper, measuring 210mm by 297mm.
A quick conversion between inches and millimetres shows the two sizes aren’t all that different:
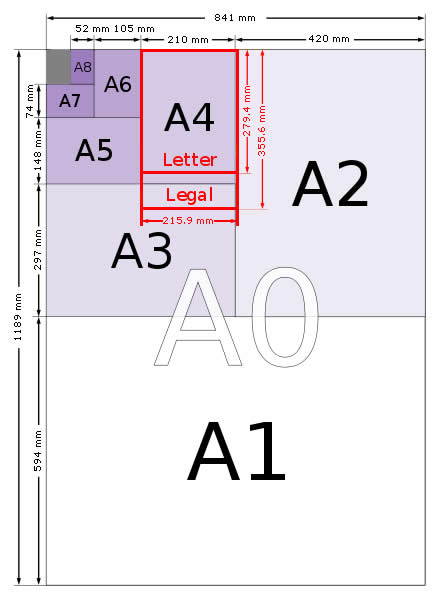
-Millimetres-- -Inches------- Width Length Width Length A4 210.0 297.0 8.26 11.69 Letter 215.9 279.4 8.50 11.00
And a scale representation of each page size reinforces the closeness of the two paper sizes.

A4 isn’t an arbitrary size.
A4 is part of the ISO 216-series of related paper sizes known more commonly as the A-series. This series starts with the large A0 sheet and a quick look at this large sheet of paper shows why these various sheets are the sizes they are.
A0 sheets of paper are 841mm by 1189mm. Again, apparently arbitrary. Multiply the two numbers together, however, and it becomes a little clearer: 841 * 1189 = 999,949mm squared or 0.999949m squared (ie just a smidgen under a square metre of paper). For all practical purposes, an A0 sheet contains a square metre of paper.
So why not make it a 1m by 1m sheet? Because of another non-arbitrary consideration: the aspect ratio or relationship between the height and width of each sheet.
1189/841 = 1.413793103448276. Not particularly memorable, unless you happen to be maths-geeky enough to see the similarity between it and √2 (the square-root of 2, an irrational number which starts thus: 1.414213562373095). Round both numbers to four significant figures and you get the same value: 1.414.
So, the aspect ratio of an A0 sheet of paper is, again for practical purposes, one as to the square-root of two or 1:√2. And again, I hear the cries: ‘so what!’
A ratio of 1:√2 is more than a mathematical oddity. It doesn’t have a nifty name, like the famous Golden Ratio or Golden Mean. It does, however, have a nifty property. Divide a rectangle with sides 1:√2 along the longest side and the smaller rectangle you create has the same aspect ratio. (Markus Kuhn suggested in correspondence we call the ratio the Lichtenberg Ratio, after Professor Georg Christoph Lichtenberg, the German enlightenment figure who first proposed the ratio as a basis for paper formats in 1786.)

We can easily, and quickly, derive all the other A-series sizes by folding or dividing thus:
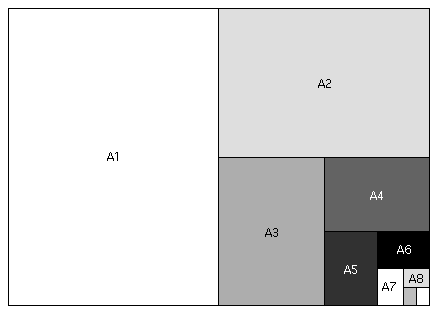
In less visual terms, any sheet of A-series paper is as long as the next-larger sheet is wide and half as wide as the next-larger sheet is long.
Sheet name Width (mm) Length (mm) A0 841 1189 A1 594 841 A2 420 594 A3 297 420 A4 210 297 A5 148 210 A6 105 148 A7 74 105 A8 52 75
There are other benefits to this relationship between paper sizes, not least of which is when you want to scale a particular layout. If you’ve ever wondered why photocopiers offer a 71% reduction option wonder no more: 0.71 is approximately equal to (√2)/2 or √0.5. This makes it perfect for reducing an A3-layout onto an A4 sheet, or an A4 layout onto an A5 sheet or, more commonly, reducing two A4-sheets side-by-side — say in a journal — neatly and without fuss onto one A4-sheet. The equally common 141% option is, of course, perfect for enlarging from one A-series sheet up to the next (eg A4 to A3). Most important, because each sheet has the same aspect ratio, objects retain their relative shapes: squares don’t become rectangles and circles don’t become ellipses.
Add in a clear connection to the metric (or, more properly, the SI) measuring system and the rise in popularity of A-series paper is fairly easy to understand: as the world has slowly but surely gone metric, so A-series paper has become more popular. In Australia, for example, the metric system was adopted officially in 1974, the same year A-series paper (and related series such as the C-series for envelopes) started to become the standard.